De 01 a 03 de setembro/2021, em formato virtual, Paulo Cella e Flávia Augusta Padovani, participaram da “7th Internacional Conference Tailings Managment 2021”, com a publicação de um artigo abrangente, sobre o comportamento de rejeitos hidráulicos em algumas minerações do Brasil: “Five Brazilian Tailings: from laboratory and field data towards safer design criteria”.
Um evento que teve a participação de mais de 480 delegados de 18 países. Nesta ocasião, 76 apresentações relacionadas aos desenvolvimentos e melhores práticas no transporte, descarte, controle e monitoramento de instalações de armazenamento de rejeitos convencionais, espessados, pastosos e filtrados.
Orgulhosamente compartilhamos o artigo.
Paulo R. C. Cella 1* and Flávia A. Padovani 2*
1. BVP Engenharia, Brazil
2. BVP Engenharia, Brazil
ABSTRACT
Gold and iron ore tailings from mining operations in Brazil contain predominantly sand and sandy silt particles. Given the difficulties inherent to obtaining fully undisturbed samples, the geotechnical characterization of mine tailings is based mostly on piezocone soundings and comprehensive laboratory testing using remolded samples to a range of densification conditions compatible with the state parameter from cone penetration tests. This paper examines the liquefaction potential of five samples of tailings from processing iron and gold ores at different mining locations as well as discussing an integrated interpretation of stress-strain and stress paths, in light of the critical state framework (Jefferies and Been, 2016) and the empirical approach (Robertson, 2010, 2012, 2016, 2018).
The critical state line was determined using conventional isotropically consolidated undrained and isotropically consolidated drained tests under loose and dense conditions. The reconstituted samples were prepared using the moist tamping method with careful percolation under very low hydraulic gradients at the base and the top of the specimens, followed by application of back pressure to achieve full saturation. The instability line was defined over the excess pore pressure stress paths attained from samples consolidated to 10-15% below the maximum void ratio, i.e., to a very loose state. The stress paths of dense and loose specimens were closely reviewed and fitted to a line to reveal the boundary between contractive and dilative behavior.
The field state parameters derived from piezocone soundings were taken into account in the setup of a comprehensive laboratory testing program. The undrained brittleness index and the initial-critical stress ratio were also discussed in this paper whenever specific thresholds indicating changes from brittle to less brittle or less unstable behavior were achieved.
INTRODUCTION
In general terms, mine tailings are hard particles crushed/grinding to sand and/or smaller particle sizes processed into slurry for deposition in a storage facility. Most of the iron ore in Brazil occurs in the form of friable itabirite. As a result, most beneficiation operations require minor grinding, with processing revolving chiefly around flotation or magnetic separation. Recent increases in the occurrence of hard itabirite have elevated grinding requirements and consequently pushed processing costs up. Gold ore processing comprises crushing and grinding, followed by separation using cyclone technology. Cyclone technology allows the separation of tailings into coarse and fine fractions, respectively known as underflow and overflow.
The tailings resulting from the processing of gold and iron ore in Brazilian mining operations contain mostly sand and sandy silt, known for their low or nonexistent plasticity. Given the difficulties inherent to obtaining fully undisturbed samples, the geotechnical characterization of mine tailings is based mostly on piezocone soundings and comprehensive laboratory testing using remolded samples to a range of densification states, since critical states involve large strain behaviors.
Critical state testing of tailings has gained attention in recent years as it allows the soil behavior to be defined as a function of properties that are independent of densification (e.g. critical friction angle) and for providing the boundary of contractive-dilative behavior, a key design and construction parameter in many branches of engineering. However, the path from geotechnical characterization in a laboratory and on the field to the development of sound, reliable standards and design criteria with practical use has been less than straightforward. The challenge lies in acquiring a sense of how tailings brittleness affect the safety of any given TSF (tailings store facility). This paper attempted to address this question in light of the behavior of five samples of brittle tailings taken from gold and iron ore mines in Brazil characterized based on the critical state framework.
TAILINGS GEOTECHNICAL CHARACTERIZATION
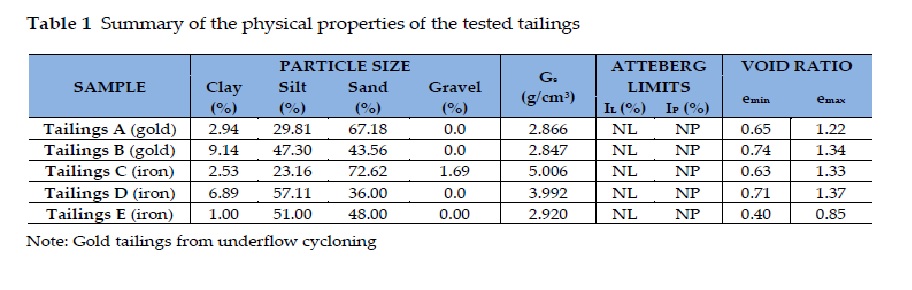
The testing program was designed to assess the behavior of gold and iron ore tailings samples via the critical state framework (Jefferies and Been, 2016) and the empirical approach (Robertson, 2010, 2012, 2016, 2018). Table 1 shows a summary describing the physical properties of the tailings samples, which contained primarily non-plastic sand and silt-size particles. Figure 1 shows the particle size distributions characteristically seen in the tailings analyzed in this paper.
The maximum void ratios (emax) presented in Table 1 were obtained from settling tests, since they characterize the sub-aerial disposal of tailings better than the standard soil test. In the settling test, void ratios and solid contents were calculated based on the volumes read from a conventional graduated container.
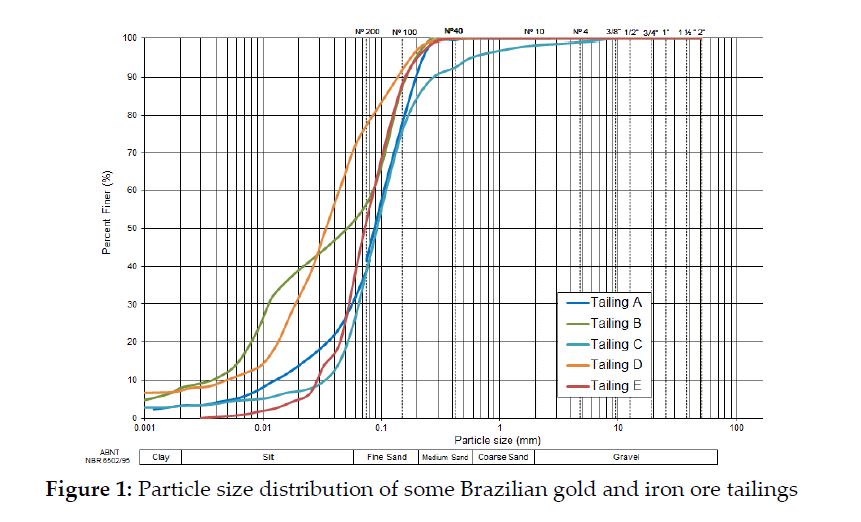
Several experimental studies developed with different types of tailings (Silva, 2008) have shown that the settling test can be satisfactorily used to determine the maximum void ratio. In addition, the final void ratios after stabilization were very close or equal to one another in tests with samples with different initial solids contents taken from the same specimen (Pereira, 2017).
In the testing program presented in this paper, the maximum void ratio was first calculated using the hand scoop and the sedimentation test methods. The obtained results indicated that the higher the specific gravity of the soil particles (Gs), the greater the difference between the two methods, as seen in Table 2.
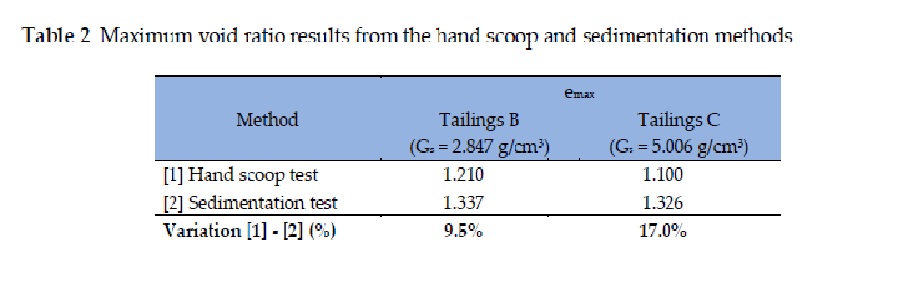
Since the reconstituted samples for the triaxial tests were prepared using fractions of the emax as a reference (i.e. densification), the use of the most accurate void ratio became an essential requirement to assess compression tests results.
TAILINGS CRITICAL STATE BEHAVIOR
Instability Line
The testing program included isotropically consolidated undrained (ICU) and isotropically consolidated drained (ICD) tests for initially loose and dense conditions. The reconstituted samples were prepared using the moist tamping method with careful percolation under very low hydraulic gradients at the base and the top of the specimens. After several days, bubbling decreased to a minimum or stopped completely. Then, backpressure was applied to allow full saturation and Skempton’s B̅ values of 0.97-1.0 were achieved.
The program started with ICU tests featuring the loosest specimens at confining pressures of 100, 200, 400, 800, and 1000-1200 kPa. The critical state locus (CSL) was first delineated upon stationary conditions of deviatoric stress and pore pressure. This permanent state was not recognized in all undrained tests. The confining stresses used in the ICD tests were picked initially from mid-range confining stress values used in the ICU tests with critical state loose specimens. Critical state dense samples were subsequently tested under a wider range of confining pressures in order to attain the best fit with the contractive-dilative boundary on both tails of the CSL. The void ratio computed at the end of the ICD tests was averaged over specimen deformation height. By using low to moderate confining stresses in the ICD tests, the resulting consistent strain distribution enabled a more accurate delineation of the CSL than if denser and highly confined samples had been used, in which shear strain would have concentrated in a localized band thus causing larger void ratio differences across the specimen.
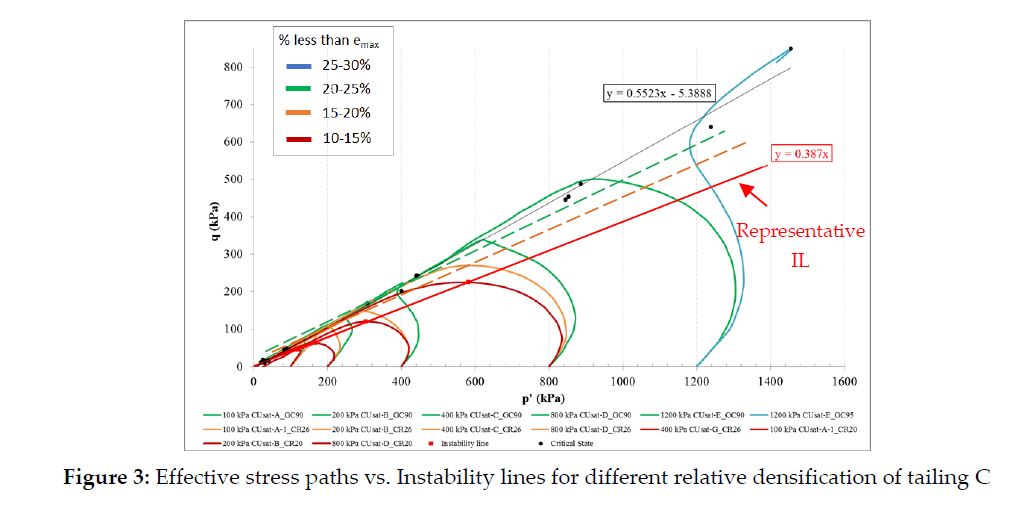
The instability line (IL) for the sandy and silty tailings analyzed in this paper was defined over the effective stress paths for samples consolidated to 10-15% below the maximum void ratio (i.e., very loose state). Figure 3 illustrates the range of densification investigated relative to e_max.
The instability line represents the maximum effective strength under undrained loading. This boundary is achieved the instant the rate of excess pore pressure is maximum under undrained loading conditions (Been, 2016). The term instability refers to the onset of increased plastic strain rates due to the inability of a soil element to sustain a given load or stress (Wanatowski; Chu and Loke, 2010). Figure 2 shows the instability lines obtained for each type of tailings tested, with dashed lines representing the paths used to define the IL (this differentiation was not applied to Figure 2b, since all effective stress paths were considered in the definition of the IL). Figure 2 also shows the critical state line of the tailings.
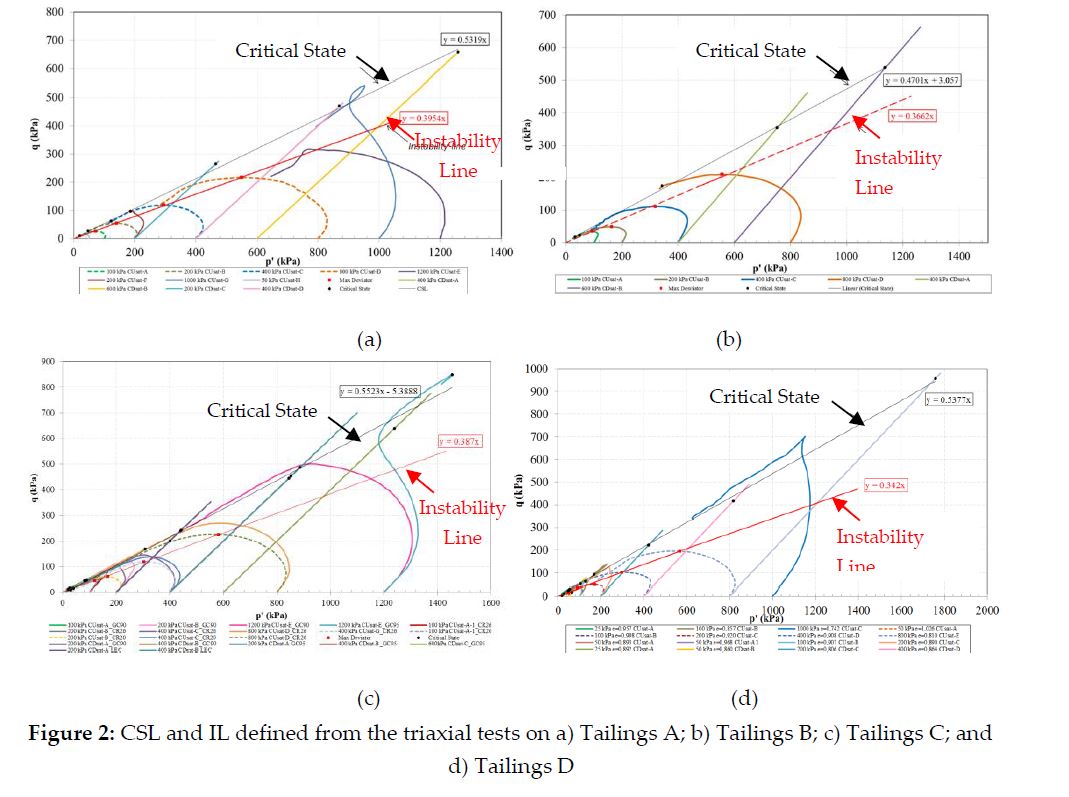
The Critical State (CS) envelope represents the ultimate condition that can be attained after shearing (Jefferies and Been, 2016), if the initial state of the specimens is such that they can withstand significant strain in a physically stable manner. It is important to mention that some tailings samples with specific initial void ratios were unable to deform to the critical state, since the region between the CSL and the IL represents a potentially unstable zone.
The results showed in Fig 2c for confining stresses of up to 1.2 MPa typify the role of purely contractive behavior under undrained loading for the loosest samples (consolidated to 10-15% below the emax), which generated excess pore pressures beyond the peak (i.e., IL). A denser specimen of Tailings C under the same confining stress of 1.2 MPa had an S-shaped stress path.
Although it has been argued that the IL does not stand for an intrinsic soil property since it may change with the state parameter of the soil, the applied mean effective stress and its elastic and plastic properties (Jefferies and Been, 2016), the results showed that the IL slope is an important design parameter to be pursued, which reasons are discussed in the next Section. The critical state friction angle (i.e., the critical state line), in turn, is not affected by changes in density, thus representing a unique relationship between shear stress, normal effective stress, and critical void ratio (Robertson, 2017). Figures 3 and 4 show some ICU tests of Tailings C specimens with different consolidation ratios and under the same mean effective stress, p’. Brittleness is remarkable, even under undrained loading conditions.
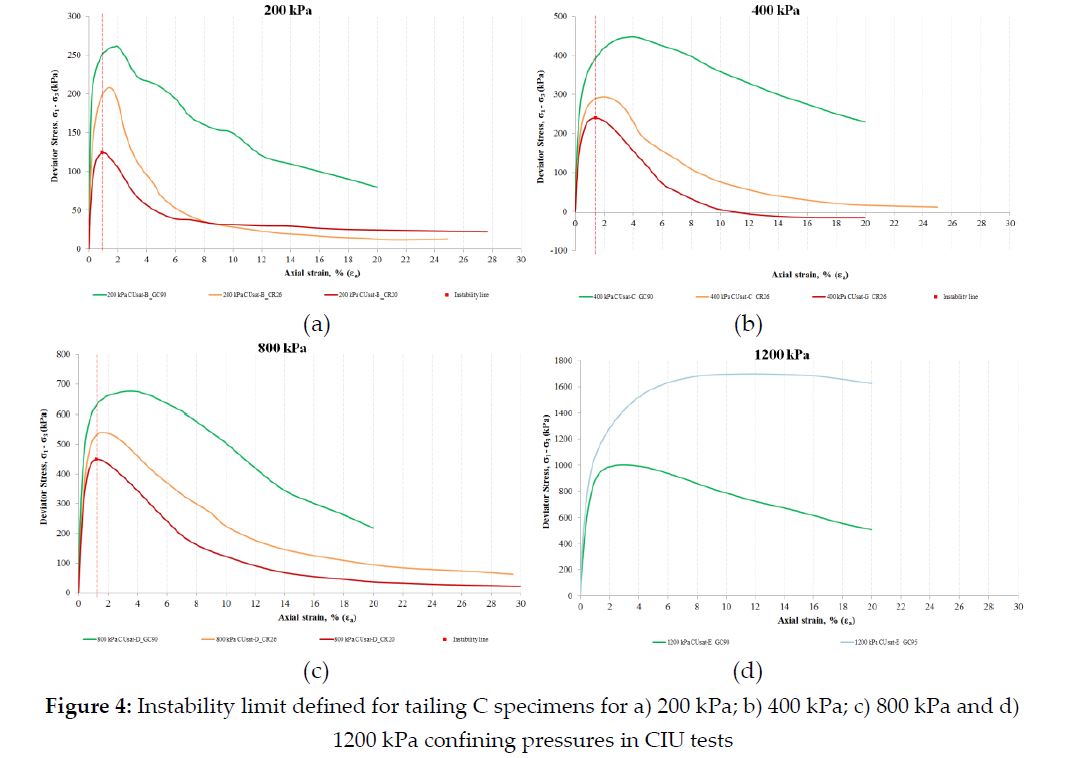
For the same confining pressure, Figure 4 shows that the higher the initial void ratio, the lesser the soil deforms to the peak strength and the higher the brittleness is.
Critical State Line
The critical state line (CSL) is defined first as the relationship between void ratio in the critical state (ec) and mean effective stress (p’c = (σ′1+2σ′3)/ 3). It usually represents the boundary between i)contractive (i.e., a loose state, thus potentially susceptible to liquefaction) and ii) dilative (i.e., a dense state, potentially not susceptible to liquefaction) behavior. Indeed, the boundary that separates liquefaction potential is defined with aid of an auxiliary line that runs parallel to the virtual critical state to define a narrow strip delimited at a void ratio 0.05 lower than ec. The vertical distance from the initial ‘in situ’ state to the CSL is designated as the state parameter () of the material. can be estimated through empirical correlations between tip resistance and sleeve friction measured in piezocone penetration tests. Two methods for the estimation of the state parameter are briefly discussed in the next Section.
Conventionally, the critical state is represented in the e – log (p′) space, using the semi-log form (Jefferies and Been, 2016):
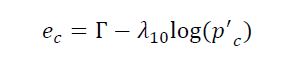(1)
Or by the improved (curved) CSL idealization:
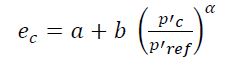(2)
Where ecrepresents the critical void ratio, Г is the critical state void ratio at the reference pressure, p’, of 1kPa; and λ10 is the slope of the CSL in a semi-log scale. Parameters 𝑎, 𝑏 and 𝛼 are fitted to match test results, and is taken as 1 atm, i. e., 101.32kPa (Schnaid, 2020).
Besides Г and λ10, the critical state is also represented by parameter M, which denotes the maximum shear stress ratio (q = σ1 – σ3) to the corresponding mean stress (p’c), M = qc/p’c. M is conventionally defined under triaxial compression conditions and can be related to the critical state friction angle 𝜙c by (when M = Mtc):
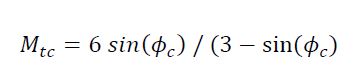(3)
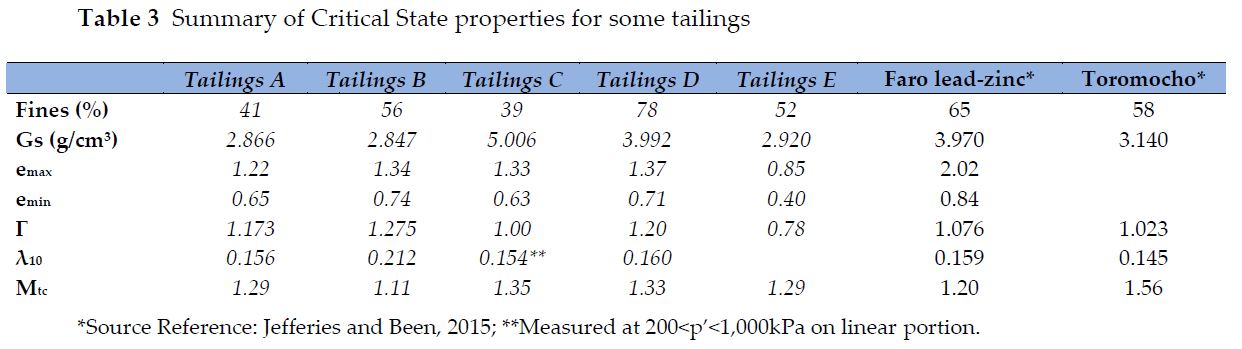
Figure 5 shows the CSL for the samples of Brazilian tailings considered herein. Notice that for Tailings C and E (Dawson et al. 2019), the critical state line was represented by a curved line, whereas for Tailings A, B and D the CSL was best fitted against an approximately linear boundary. See also the CLS for bauxite tailings by Schnaid 2020. Table 3 summarizes the critical state parameters obtained for the tailings and offers a comparison against typical values reported by other authors for similar materials (i.e., silty or sandy tailings).
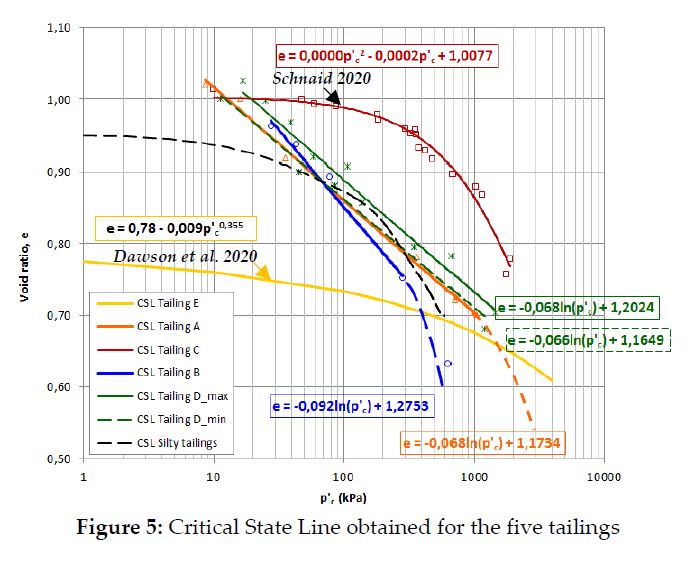
In the tests with Tailings A, a CDsat-C sample (σ3c= 200 kPa) was prepared with an initial void ratio very close to the critical state condition, which presented limited strain softening. For this condition, the material underwent limited volume decreases, with an initial and final path coinciding with the CSL. Figure 6a shows the Tailings A stress paths in the e – log p’c space.
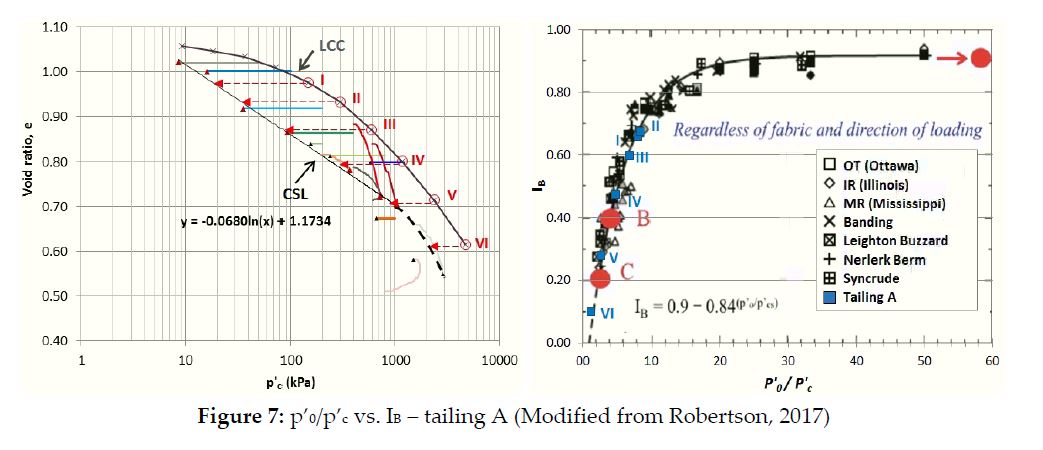The CSL inflection point shown in the dashed line was inferred from the expected parallelism in relation to the Limiting Compression Curve (LCC). The LCC was determined based on consolidation tests performed to stresses above 3 MPa on very loose samples. The isotropic consolidation line obtained during the consolidation phase of the triaxial tests may also be used to infer the CSL at higher stress levels. In the studied tailings samples, the curvature point of the CSL varied significantly from 300kPa to 1000kPa.
In practical terms, it represents the limiting stress for brittle behavior, when the p’LCC/p’C stress ratio is less than about 4 and the brittleness index (IB) is lower than 0.4 (Robertson, 2017). Therefore, the IB and the p’0 /p’c ratio correlate as follows:
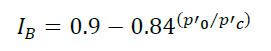(4)
Where, p’0 is the current in-situ mean effective stress and p’c is the mean effective stress at the CS for the same void ratio (Robertson, 2017). LCC represents the maximum virtual locus of p’o for a given very loose initial condition under isotropic consolidation.
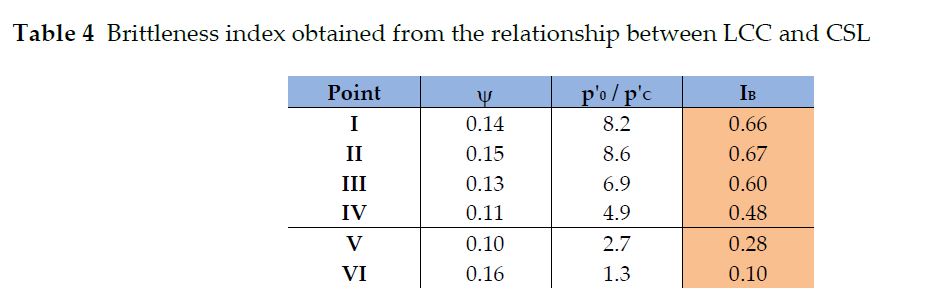
Considering the CSL and the LCC for Tailings A, Table 4 shows that beyond the curvature (point V), IB and the p’LCC/p’C ratio presented values lower than 0.4 and 4, respectively, even with increases in . Figure 7 indicates i) selected points for brittleness assessment and ii) the trend line for brittleness index vs. stress ratio, where IB increases with the p’LCC/p’C ratio.
STABILITY ASSESSMENT
When dealing with brittle materials, a significant gap must be bridged to connect laboratory test findings and site-specific conditions, so that not only reliable design parameters are defined, but also appropriate safety margins must be taken to address the high risks inherent to tailings impoundments.
Large-scale chamber tests and a wide range of boundary conditions and sample densification were used during piezocone tests researched by Jefferies and Been (2016). The cavity expansion method described by these authors was applied to connect cone penetration test data to laboratory triaxial shear strength test results. The state parameter as computed from seven triaxial-related parameters was thus used as a powerful descriptor of site conditions applicable primarily to soils in which the void ratio and confining stresses govern the undrained behavior on either loose or dense of soils in the critical state. Plewes et al. (1992) also developed a correlation to compute the state parameter from piezocone data by using two empirical parameters derived from the critical state.
Based on the approach developed by Jefferies, a Technical Panel (Robertson et al. 2019) prepared Figure 8 to show the frequency distribution of the state parameter from piezocone soundings carried out as part of the investigations on the failure of Dam I (ref.). In order to draw comparisons against the test results obtained by the Panel, the authors of this paper collected disturbed tailings samples from tailings remaining at scarps that bound the collapsed area in the dam site. The collected samples represented the coarse fraction (silty sand) of the tailings. They were remolded in a way to represent the state parameter distribution condition, i.e as loose as +0,10 to +0,15 and tested under undrained and drained loading conditions.
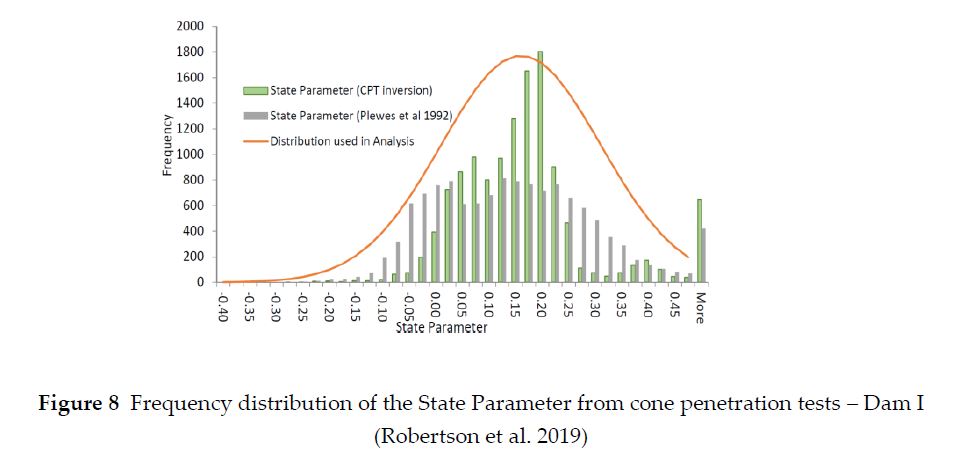
The undrained stress paths for the tested tailings are shown in Figure 2, along with the critical state envelope and the instability line or phase transformation boundary. The IL envelope was defined for Tailings C on a loose condition (RD 35%) in the first quartile. The IL envelope is the ratio Supeak/p’ = 0.39 for isotropically consolidated specimens. The IL was traced through the apex of the excess pore pressure hoops and slightly before the reversion path from negative to positive pore pressure when denser samples, higher confining stresses or both were present.
The practical significance of determining the IL for a sufficiently loose condition is that the stress path, even for an initially dilative granular soil, responds predominantly in a contractive fashion below the IL. Above the IL, dilation may occur only in free draining or dense of the critical state. In the case of initially contractive tailings, there is no dilation even above the IL, with physical instability of the sample can be attained as shown on track 0-1-2 in Figure 9.
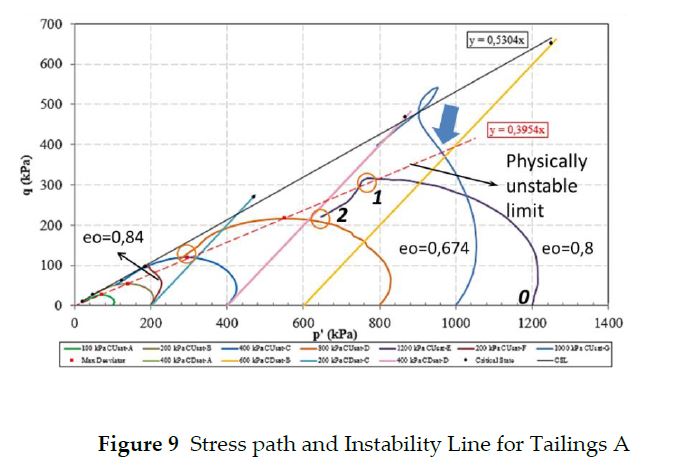
Path 0-1-2 denotes physically unstable behavior of porous, contractive tailings, which occurs mainly at higher stress levels. It is indicative of high brittleness, strain-softening behavior, and there is no post-peak condition above the maximum undrained strength envelope or IL. Notice that samples under the lowest stress levels were able to withstand post-peak conditions above the IL up to the Critical State envelope, not without losing shear strength rapidly in a clear tendency to liquefaction.
Safety consideration relies on the ratio of mobilized shear stresses to the undrained strength envelope. Though stresses that develop across a potential failure surface are never uniformly distributed over its length, the limit equilibrium (LE) method carries an inherent lack of accuracy when analyzing brittle materials, since it is essentially an averaging method. This feature of limit equilibrium is even more inaccurate for soils loose of CSL because they contract more. Specific areas of tailings impoundments near the dam wall may be mobilized to values equal or close to maximum strength in weaker layers, while some portions of potential failure surface still remain below maximum strength. Such scenario reveals that LE might be unreliable for dams in which the liquefaction potential is debatable or when even subtle, progressive failure is an issue. However, at higher stresses, usually above 1,000 kPa, as long as brittleness tends to decrease, the peak approaches the large strain condition, thus making LE more accurate. In short, LE may not be particularly reliable for materials that reach their peak undrained strength under low strain (i.e., 1-2%) on account of a progressive failure mechanism. In these cases, LE is always a conservative lower bound for large strain condition or post-liquefaction strengths.
Figure 10 illustrates the classical paths of static triggers that cause undrained failure and that may potentially lead to flow liquefaction. Exception is path 5 to be discussed further on. All such paths depart from an idealized locus of mobilized stresses named ‘in situ state,’ attained at the dam construction completion. Let us assume that the ‘in situ state’ lies fairly far from the maximum undrained strength envelope or the IL or the phase transition boundary, as shown in Figure 10.
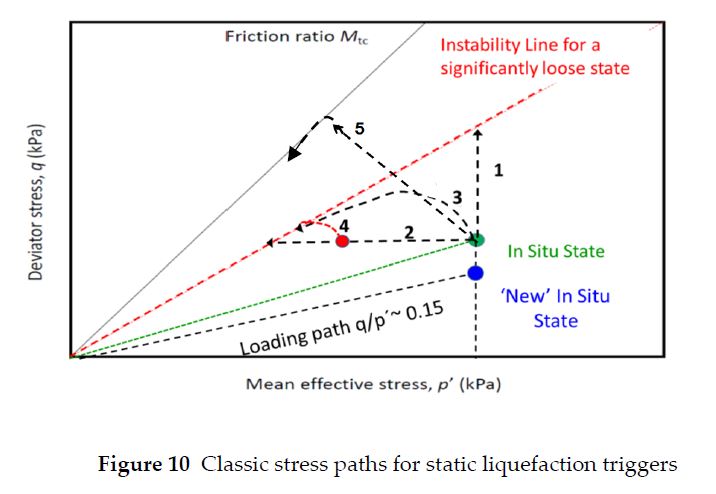
In simple terms, path 1 denotes a very fast overloading of the dam (i.e.B̅ ≈1); path 2 shows a gradual rise of the water table; and path 3 describes any shear-induced undrained mechanism. Each represents a mechanism that acts in isolation, although this rarely occurs. Phreatic surface rises may bring the ‘in situ’ state closer to the IL, and even minor undrained shear mechanisms may combine to eventually cause the failure of the dam.
Regarding the Fundão failure, Morgenstern et al. (2016) have proposed lateral extrusion mechanism across a thicker slime layer, at depth of 20-25m, to explain the collapse of the dam. According to them, the failure would have been caused by progressive relief of the confining stresses in an overlying sandy layer which ultimately failed at once. Numerical modeling of staged construction (raises) using NORSAND showed the maximum horizontal displacement would has reached 340mm at 80% of the Mobilized Instability Ratio – a limit for the sake of numerical stability. Such displacement slightly below the peak implies 0.3% of the length of the sheared portion. Such very small ‘strain to peak’ of the numerical model concurs with the results of isotropic drained triaxial tests conducted under decreasing σ3 and constant σ1 stress condition. Those tests imposed gradual reduction of the mean stress and have shown a gentle increase of axial strain up to 0.5%, then a change to a phase of strain under almost constant mean stress. The specimens collapsed in critical state condition due to the drained nature of the test. Therefore, lateral extrusion – an essentially drained unloading mechanism – has been shown to become a potential trigger for progressive failure mechanism that ultimately can lead to liquefaction with very small strain, apparently lower than those in shear-induced undrained mechanism, and even for brittle tailings slightly loose of critical state.
The more brittle the material and the lower the strain to peak, the less the mobilized stresses should be allowed to grow towards the IL, i.e., the undrained strength envelope for loose states. It must be emphasized that it is not enough to take care of QA/QC by allowing excess pore pressures to fully dissipate before resuming the next loading stage and so forth. What if a drained path is imposed to allow the stresses to grow consistently above the IL? This condition means that the dam would not withstand even a minimal additional undrained static trigger. Therefore, preventing the build-up of excess pore pressure as the dam is raised alone might not preclude undrained failure to occur from shear-induced mechanism. In situ stresses must be kept significantly below the IL.
The five samples of tailings tested for Mtc and IL envelopes showed that the choice, in early design stages, of a looseness state that matches void ratios approximately 15% lower than the maximum void ratio is apparently a sound approach to test for the Supeak/σ′v ratio prevalent in sub-aerial disposal of tailings in beach fronts. Figure 11 shows a Supeak/σ′v ratio verified by the Report of the Expert Panel on the Technical Causes of the Failure for Feijão Dam I tailings (Robertson et al. 2019), which is given by:
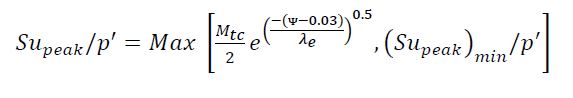(5)
Where (Supeak)min/σ′v is the value determined for > +0.15. For Feijão Dam I tailings, the Panel reported a (Supeak)min/σ′v of 0.16 for averaged grain size compound.
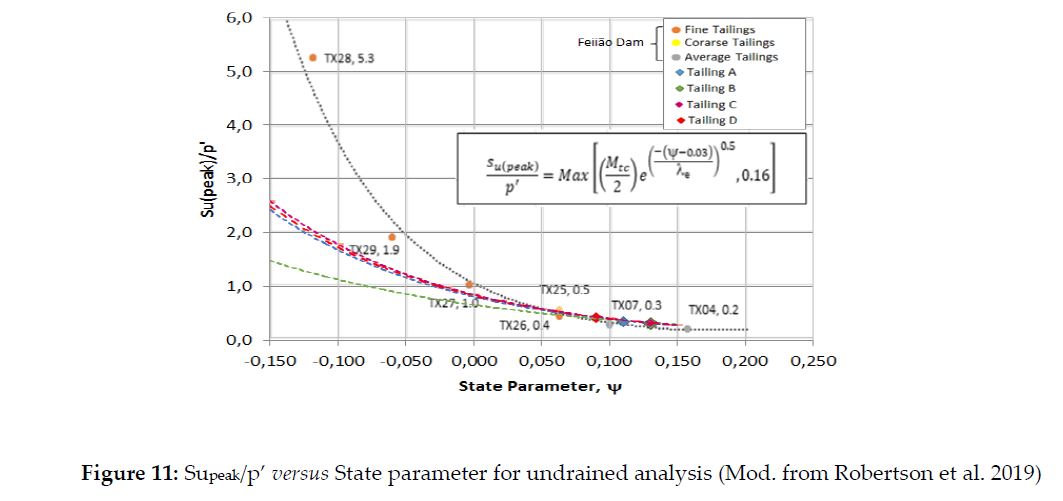
Tailings A, B, C and D were plotted in Figure 11 against the Feijão dam site tailings (Panel). In the four tailings samples the power law tended to match nearly +0.07 using Supeak/σ′v derived from within the +0.08 to +0.13 range (i.e., for void ratios around 15% below the maximum). Larger void ratios appeared to fit an asymptotic trend line with very small variations beyond a state parametergreater than +0.13 as shown in Figure 11. Hence, one may conclude that laboratory tests using remolded samples to a range of densification within +0,10 < < +0,20 allow for a safer definition of the IL on which LE analyses should be based.
Moreover, testing tailings to consider a wider state parameter range is time consuming and hardly pursued in most of tailings impoundment designs. Finer gradation and subaqueous deposition, however, can turn out significantly lower Supeak/σ′v ratios, as described by Shuttle and Jefferies (2016) for silty tailings.
Again, the larger the brittleness index and the lower the strain to peak, the more the limit equilibrium method can be misleading due to increasing concentration of stresses as the dam become larger. Given its averaging nature, LE may fail substantially whenever progressive failure is a possibility. In cases where only LE is used, use of the IL envelope tested for very loose states is recommended, along with the addition of a safety margin on top of the standard-defined factors of safety. LE is a relatively reliable method regardless of the level of brittleness when stability analysis is conducted in conditions of large strain (residual strength) or high stress levels (i.e., deep-seated failure).
A second limitation of LE relates to the unsuitability of the method at representing the mechanism of flow liquefaction and its propagation throughout the soil mass. Upon subtle loss of physical stability at the onset of liquefaction, even if it affects only a portion of the facility, the soil element is rendered unable to effect a reaction against the sum of unbalanced forces from contact slices. The basic assumption of LE formulation relies on a solution in which the unbalanced forces transfer successively from upper to lower slices along the potential failure surface. Such mechanic disrupts when a portion of soil mass gets collapsed. A 2D numerical method able to implement an experimental user-defined function for the rate of strength loss after peak is often sufficient to sort out the limitations of LE in cases of progressive failure.
Safer loading paths to a ‘new in situ state’ as shown in Figure 9 may be achieved by making the slope of the dam gentle enough to avoid conditions marginally approaching the IL envelope, whenever brittle behavior is an issue.
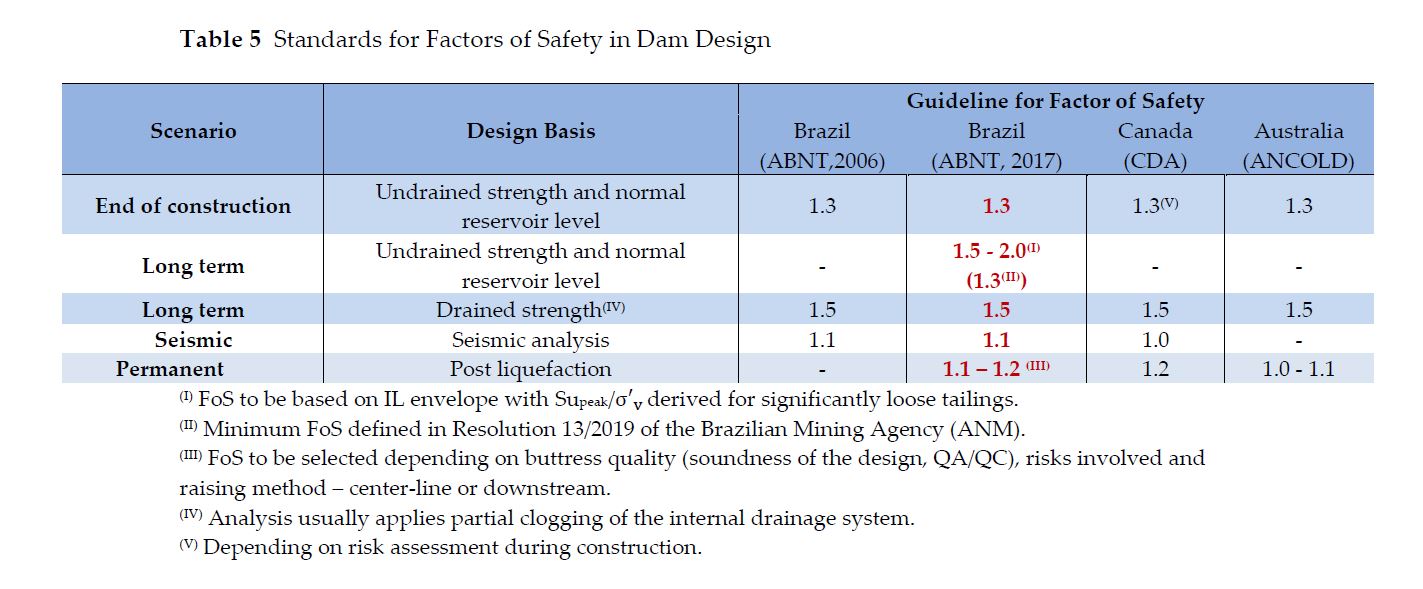
Table 5 presents a summarized comparison between requirements set out in the Brazilian Standards and the standards published by the CDA and the ANCOLD on the recommended Factors of Safety (FoS) for drained and undrained analysis. The authors of this paper added the Long Term, Undrained Analysis to consider the increases needed in safety margins in scenarios of sub-aerial disposal of brittle tailings. If only 2D LE analysis is performed, then a FoS sufficiently above 1.5 is strongly recommended.
CONCLUDING REMARKS
The development of a comprehensive triaxial testing program to cover the wide array of parameters required to compute site-specific state parameters using the approach proposed by Jefferies and Been (op. cit.) should be seriously considered in the design of large and/or risky projects or when responses consistent with highly brittle behavior are identified in exploratory tests.
It must be also emphasized that the opinion of the Technical Panel while addressing the failure of Dam I in the Córrego do Feijão Mine was that existing empirical relationships derived from piezocone penetration tests based on historical cases could not always be inferred for tailings with high densities, any type of bonding, cementation or other specific features that may produce behavior that is dissimilar to that of the tailings in the database.
Regardless the remarkable differences among the tested tailings concerning their critical state parameters (Mtc, λe), the undrained strength ratios have shown a meaningful convergence to a narrow range as the tailings were tested at significantly loose condition.
In all TICU tests within +0.08 to +0.10 loose of CSL or higher, the stress paths developed a typical excess pore pressure hoop, remarkably contractive throughout the stress states below or above the Instability Line. In some tests, the breakdown observed nearly the apex of the stress path suggests the onset of the unstable behaviour around the IL.
Static liquefaction triggers are fairly discussed in the literature while their nature is better known. However, knowledge on the magnitude required to initiate the collapse across a real deposit is strongly dependent from operation factors and far beyond designer consideration. A defensible manner to mitigate such uncertainty is keeping the typical loading path away from the IL by making the overall slope sufficiently gentle. It is easy to see that the loss of impoundment storage is not sensitive to smoothing the global slope when the tailings dam axis is located further away from the waterhead.
Factor of Safety should be decided on case by case basis comprising not only uncertainties on the mobilized undrained parameter but should also consider i) the potential for progressive failure increase with the brittleness and the smallest is the strain-to-peak; ii) the strain softening rate and
the residual strength; iii) limitations of the stability analysis method and iv) how reliable are both the depositional history and the stratigraphy complexities of the deposit, which ultimately govern the mechanisms of failure.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the invaluable contributions provided by Tadeu Castro at Chammas Laboratory during the development and implementation of the laboratory testing program.
REFERENCES
Been, Ken, Mike Jefferies, and Joseph Hachey. 1991. The critical state of sands. Géotechnique 41, No 3, 365-381.
Been, Ken. 2016. Characterizing mine tailings for geotechnical design. Geomechanics Society. J. 50, No. 4, 59–78.
Dawson, Richard, Andrew Burgin, Mathieu Walcowich, Jose Bernardo and Anelisa Vasconcelos. 2019. Laboratory and CPTu Characterization of Samarco Sand Tailings. Proceedings of Tailings and Mine Waste, Vancouver, Canada.
Jefferies, Mike and Ken Been. 2016. Soil Liquefaction: A Critical State Approach. CRC Press. Second Edition.
Morgenstern, Norbert R., Steven G. Vick, Cássio B. Viotti, Bryan D. Watts. 2016. Report on the immediate causes of the failure of the Fundão Dam.
Pereira, Eleonardo Lucas. 2017. Estudos das características de compressibilidade e adensamento de rejeitos de fosfato de baixa densidade como uso de técnicas experimentais de laboratório e de campo. Federal University of Ouro Preto.
Plewes, H. D., M. P. Davies, M. G. Jefferies. 1992. CPT based screening procedure for evaluating liquefaction susceptibility. 45th Canadian Geotechnical Conference.
Robertson, Peter, Lucas de Melo, David J. Williams and G. Ward Wilson. 2019. Report of the Expert Panel on the Technical Causes of the Failure of Feijão Dam I. Appendix E.
Robertson, Peter. 2010. Evaluation of Flow Liquefaction and Liquefied Strength.
Robertson, Peter. 2012. Interpretation of in-situ tests – some insights. J.K. Mitchell Lecture, ISC’4.
Robertson, Peter. 2016. Cone penetration test (CPT)-based soil behaviour type (SBT).
Robertson, Peter. 2017. Evaluation Of Flow Liquefaction: Influence Of High Stress. PBD III Vancouver.
Schnaid, Fernando. 2020. The Ninth James K. Mitchell Lecture: On the geomechanics and geocharacterization of tailings. James K. Mitchell Lecture.
Shuttle, Dawn and Mike Jefferies. 2016. Determining silt state from CPTu. Geotechnical Resarch, 3(3), 90-118.
Silva, Wander Rodrigues da. 2008. Nova metodologia para determinação de propriedades de sedimentação e adensamento de rejeitos de mineração. Federal University of Viçosa.
Wanatowski, Dariusz, Jian Chu and Wai Lay Loke. 2010. Drained instability of sand in plane strain. Canadian Geotechnical Journal. J. 47: 400–412 (2010).